Lecția 24. FUNCȚII – pregătirea Evaluării Naționale
Autor quiz: Prof. Mihaela Molodet
• Noțiuni de reamintit
– Dacă A și B sunt două mulțimi nevide, iar
este o corespondență care asociază FIECĂRUI element din A UN SINGUR element din B, spunem că avem o funcție definită pe A cu valori în B. Scriem
sau
– A se numește DOMENIU (de definiție), B se numește CODOMENIU (domeniu de valori)
– Corespondența se notează, de obicei, cu litere mici:
– Dacă A, B sunt mulțimi de numere, funcția se numește numerică.
– Cum A, B sunt mulțimi, iar acestea au 3 feluri de exprimare, pentru funcții vom avea 3 moduri de definire:
a) Prin diagrame
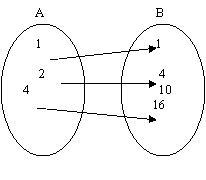
b) Printr-un tabel
c) Printr-o formulă analitică ( de obicei pentru A, B mulțimi infinite)
• Exemple de corespondențe care NU sunt funcții
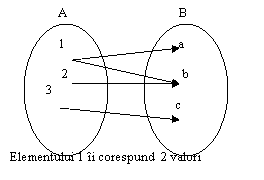
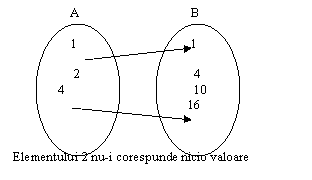
• Valoarea unei funcții într-un „punct”
Valoarea funcției în „punctul”
este notată
și se obține înlocuind, in exprimarea analitică, pe x cu
, adică
.
De exemplu:
, adică valoarea lui
în 2 este -1.
• Imaginea funcției
Este mulțimea notată
= mulțimea valorilor funcției
Evident,
De exemplu, pentru
• Funcții egale
Două funcții
se numesc EGALE dacă
Exemplu:
, sunt egale pentru că au același domeniu, același codomeniu, iar
• Graficul funcției
Este mulțimea notată
, așadar o mulțime de perechi ordonate.
De exemplu, pentru
• Reprezentarea grafică ( geometrică) a funcției
este mulțimea punctelor din plan
, unde
De exemplu, pentru
reprezentarea grafică =
Important: Deseori reprezentării grafice i se spune „grafic” pentru că există o relație biunivocă între cele două.
• Apartenența unui punct la graficul unei funcții
Evident,
De exemplu, pentru funcția
avem
Mențiune: am identificat deja cu reprezentarea grafică.
• Intersecția cu axa Ox ( a reprezentării grafice)
Este dată de soluțiile ( dacă există) ale ecuației
.
De exemplu,
– pentru funcția
nu avem intersecția cu axa Ox, pentru că funcția nu ia valoarea 0.
– pentru funcția
, avem
, deci
, fiind, așadar, intersecția cu axa Ox.
– pentru funcția
, ecuația
.
• Intersecția cu axa Oy ( a reprezentării grafice)
Dacă 0 este în domeniul de definiție, atunci
De exemplu,
pentru funcția
,
Pentru funcția
, nu avem intersecția cu axa Oy, deoarece 0 nu este în domeniul de definiție.
• Observații
– În general, se lucrează cu funcții numerice, definite analitic.
– Funcția
se numește funcția constantă,
.
– Intersecția cu axa Ox poate să nu aibă elemente, să aibă un element, mai multe elemente, sau o infinitate de elemente.
– Intersecția cu axa Oy poate să nu aibă elemente, sau să aibă un singur element.
• Riscuri (greșeli)
Să confundăm
cu
.
KIDI- sfat:
Felicitări! Ai terminat cursul!
„A N T R E N A M E N T U L KIDI-10”
Rezumat chestionar
0 din 10 întrebări finalizate
Întrebări:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Informații
.
Caraplix vrea să lanseze un virus de reduceri. Oamenii vor înnebuni și vor cheltui toți banii pe care îi au. Dezastru. Doar tu poți salva situația. Dacă vrei să-ți salvezi punctele câștigate și să apari în topurile Kidibot, trebuie să fii logat(ă). Creează-ți aici un cont sau loghează-te.
Ai finalizat deja chestionarul mai înainte. De aceea nu-l poți relua.
Chestionarul se încărcă...
Trebuie să te autentifici sau să te înregistrezi pentru a începe chestionarul.
Trebuie să termini următorul chestionar pentru a începe acest chestionar:
Rezultate
0 din 10 întrebări au răspunsuri corecte
Durată de răspuns:
Timpul a trecut
Ai obținut 0 din 0 de puncte posibile, (0)
| Scor mediu |
|
| Scorul tău |
|
Categorii
- Fără categorie 0%
-
-
Din păcate, nu ai răspuns corect de suficient de multe ori. Așa că nu ai primit nici un punct. Fii mai atent data viitoare.
| Poz. | Nume | Introdus pe | Puncte | Rezultat |
|---|---|---|---|---|
| Tabelul se încărcă | ||||
| Nicio dată disponibilă | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Cu răspuns
- Reia
-
Întrebarea 1 din 10
1. Întrebare
1 puncte
Incorect
-
Întrebarea 2 din 10
2. Întrebare
1 puncteCorect
Incorect
-
Întrebarea 3 din 10
3. Întrebare
1 puncte
Incorect
-
Întrebarea 4 din 10
4. Întrebare
1 puncteCorect
Incorect
-
Întrebarea 5 din 10
5. Întrebare
1 puncteFie funcția
Incorect
-
Întrebarea 6 din 10
6. Întrebare
1 puncteCorespondențaCorect
Incorect
-
Întrebarea 7 din 10
7. Întrebare
1 puncteFie funcția
Incorect
-
Întrebarea 8 din 10
8. Întrebare
1 puncteFuncțiile
Incorect
-
Întrebarea 9 din 10
9. Întrebare
1 puncte
Incorect
-
Întrebarea 10 din 10
10. Întrebare
1 puncte
Incorect
Ultimele articole de pe blogul Kidibot:
Îți place quiz-ul făcut de acest user Kidibot?
Click să votezi!
Ne pare rău că un utilizator Kidibot a făcut un quiz atât de slab!
Probabil că a fost sabotat de către Crocobeți. Hai să-l îmbunătățim!
Spune-ne cum putem să-l îmbunătățim.
Exemple de întrebări din quizul "Lecția 24. FUNCȚII – pregătirea Evaluării Naționale"
- Fie funcția
- Funcțiile
Loading ...
Fii Contra-Spion
Triunghiul jucăuș
Insula Roboților
Adunarea și scăderea numerelor naturale cu trecere peste ordin, 0-100. Sistemul Solar
Ghici, ghicitoarea mea!
Expresii cu caracter popular
București Capitala României
Present Continuous
Testul nr 9 – Evaluarea Națională Clasa VIII-a
