Lecția 1 – MULȚIMI – pregătirea Evaluării Naționale
Autor quiz: Prof. Mihaela Molodet
Urmărește lecția pas cu pas
Acceptă provocarea și rezolvă quiz-ul pregătit ca o recapitulare a lecției 1
Rezumat chestionar
0 din 10 întrebări finalizate
Întrebări:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Informații
.
Multi Eyes o sa-ti arunce cu gelatina pe creierul colegilor. Castiga aceasta batalie ca sa eviti asta! Dacă vrei să-ți salvezi punctele câștigate și să apari în topurile Kidibot, trebuie să fii logat(ă). Creează-ți aici un cont sau loghează-te.
Ai finalizat deja chestionarul mai înainte. De aceea nu-l poți relua.
Chestionarul se încărcă...
Trebuie să te autentifici sau să te înregistrezi pentru a începe chestionarul.
Trebuie să termini următorul chestionar pentru a începe acest chestionar:
Rezultate
0 din 10 întrebări au răspunsuri corecte
Durată de răspuns:
Timpul a trecut
Ai obținut 0 din 0 de puncte posibile, (0)
| Scor mediu |
|
| Scorul tău |
|
Categorii
- Fără categorie 0%
-
-
Din păcate, nu ai răspuns corect de suficient de multe ori. Așa că nu ai primit nici un punct. Fii mai atent data viitoare.
| Poz. | Nume | Introdus pe | Puncte | Rezultat |
|---|---|---|---|---|
| Tabelul se încărcă | ||||
| Nicio dată disponibilă | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Cu răspuns
- Reia
-
Întrebarea 1 din 10
1. Întrebare
1 puncteeste mulțimeaCorect
Incorect
-
Întrebarea 2 din 10
2. Întrebare
1 puncte
Corect
Incorect
-
Întrebarea 3 din 10
3. Întrebare
1 puncteA= { 0, 1, 2, 3}. CardA este egal cuCorect
Incorect
-
Întrebarea 4 din 10
4. Întrebare
1 puncte{ 1, 2, 2, 3, 0} este mulțime?Corect
Incorect
-
Întrebarea 5 din 10
5. Întrebare
1 puncteA= { 0, 1, 2, 3}, B={ 0, 1, 3}Corect
Incorect
-
Întrebarea 6 din 10
6. Întrebare
1 puncteEnumerați elementele mulțimiiCorect
Incorect
-
Întrebarea 7 din 10
7. Întrebare
1 puncteMulțimea literelor din cuvântul KIDIBOT esteCorect
Incorect
-
Întrebarea 8 din 10
8. Întrebare
1 puncte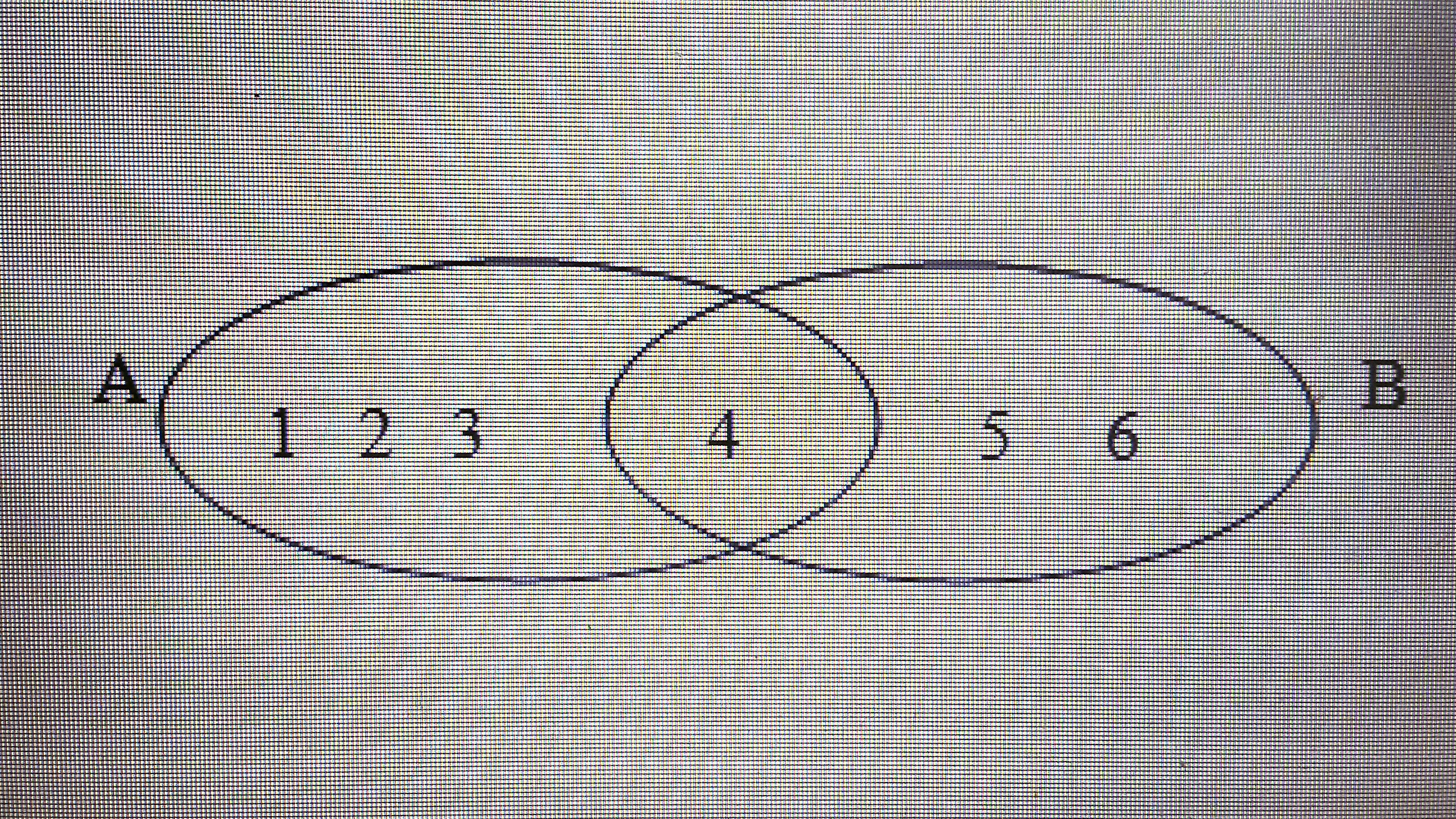Mulțimea vidăCorect
Incorect
-
Întrebarea 9 din 10
9. Întrebare
1 puncte. Atunci mulțimea A este egala cuCorect
Incorect
-
Întrebarea 10 din 10
10. Întrebare
1 puncteIntersecția mulțimilor A și B este egală cu mulțimea { 1, 2 }. AtunciCorect
Incorect
Ți-a plăcut quizul făcut de acest user Kidibot?
Click să votezi!
Ne pare rău că un utilizator Kidibot a făcut un quiz atât de slab!
Probabil că a fost sabotat de către Crocobeți. Hai să-l îmbunătățim!
Spune-ne cum putem să-l îmbunătățim.
Ți-a plăcut quizul făcut de acest user Kidibot?
Click să votezi!
Ne pare rău că un utilizator Kidibot a făcut un quiz atât de slab!
Probabil că a fost sabotat de către Crocobeți. Hai să-l îmbunătățim!
Spune-ne cum putem să-l îmbunătățim.
Exemple de întrebări din quizul "Lecția 1 – MULȚIMI – pregătirea Evaluării Naționale"
- Mulțimea literelor din cuvântul KIDIBOT este
- Mulțimea vidă
- Intersecția mulțimilor A și B este egală cu mulțimea { 1, 2 }. Atunci
Loading ...
Misiuni (Strict Secret)
Contraspionaj
Pisicile războinice Pădurea secretelor
Să ne distrăm la comunicare cu Mica Vrăjitoare
Pollyanna- Datoria de onoare
Sunt cel mai bun!
Test Internet si Comunicare Online
Armata Melcilor Zombie – Quiz final de misiune
Grupuri de vocale
Înmulțirea nr. naturale
