Lecția 2 – MULȚIMEA NUMERELOR NATURALE
Autor quiz: Prof. Mihaela Molodet
Urmărește lecția pas cu pas












Acceptă provocarea și rezolvă quiz-ul pregătit ca o recapitulare a lecției 2
Limită de timp: 0
Rezumat chestionar
0 din 10 întrebări finalizate
Întrebări:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Informații
Pregătirea Evaluării Naționale – 2020
 Uhubau a zis că e mai deșteaptă ca tine. Îi dovedești contrariul?
Uhubau a zis că e mai deșteaptă ca tine. Îi dovedești contrariul?
Dacă vrei să-ți salvezi punctele câștigate și să apari în topurile Kidibot, trebuie să fii logat(ă). Creează-ți aici un cont sau loghează-te.
Ai finalizat deja chestionarul mai înainte. De aceea nu-l poți relua.
Chestionarul se încărcă...
Trebuie să te autentifici sau să te înregistrezi pentru a începe chestionarul.
Trebuie să termini următorul chestionar pentru a începe acest chestionar:
Rezultate
0 din 10 întrebări au răspunsuri corecte
Durată de răspuns:
Timpul a trecut
Ai obținut 0 din 0 de puncte posibile, (0)
Scor mediu
Scorul tău
Categorii
-
Fără categorie
0%
-
-
Din păcate, nu ai răspuns corect de suficient de multe ori. Așa că nu ai primit nici un punct. Fii mai atent data viitoare.
Creează-ți contul KIDIBOT sau, dacă îl ai deja, loghează-te. Astfel nu vei pierde punctele castigate cu greu 🙂
maxim de puncte 10
Poz.
Nume
Introdus pe
Puncte
Rezultat
Tabelul se încărcă
Nicio dată disponibilă
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
-
Cu răspuns
-
Reia
-
Întrebarea 1 din 10
1. Întrebare
1 puncte
Cel mai mare număr par de forma cu cifre diferite este
-
-
-
-
Corect
Incorect
-
Întrebarea 2 din 10
2. Întrebare
1 puncte
-
-
-
-
Corect
Incorect
-
Întrebarea 3 din 10
3. Întrebare
1 puncte
Pătratul lui 4 este
-
-
-
-
Corect
Incorect
-
Întrebarea 4 din 10
4. Întrebare
1 puncte
Rezultatul calculului
este egal cu
-
-
-
-
Corect
Incorect
-
Întrebarea 5 din 10
5. Întrebare
1 puncte
Rezultatul calculului este egal cu
-
-
-
-
Corect
Incorect
-
Întrebarea 6 din 10
6. Întrebare
1 puncte
Triplul numărului este egal cu
-
-
-
-
Corect
Incorect
-
Întrebarea 7 din 10
7. Întrebare
1 puncte
Dând factor comun în expresia , obținem
-
-
-
-
Corect
Incorect
-
Întrebarea 8 din 10
8. Întrebare
1 puncte
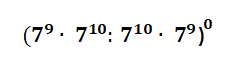
-
-
-
-
Corect
Incorect
-
Întrebarea 9 din 10
9. Întrebare
1 puncte
Rezultatul calculului 4+20:2 este egal cu
-
-
-
-
Corect
Incorect
-
Întrebarea 10 din 10
10. Întrebare
1 puncte
În calculul prima dată efectuăm
-
-
-
-
Corect
Incorect
Rezumat chestionar
0 din 10 întrebări finalizate
Întrebări:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Informații
Pregătirea Evaluării Naționale – 2020
 Uhubau a zis că e mai deșteaptă ca tine. Îi dovedești contrariul?
Uhubau a zis că e mai deșteaptă ca tine. Îi dovedești contrariul? Dacă vrei să-ți salvezi punctele câștigate și să apari în topurile Kidibot, trebuie să fii logat(ă). Creează-ți aici un cont sau loghează-te.
Ai finalizat deja chestionarul mai înainte. De aceea nu-l poți relua.
Chestionarul se încărcă...
Trebuie să te autentifici sau să te înregistrezi pentru a începe chestionarul.
Trebuie să termini următorul chestionar pentru a începe acest chestionar:
Rezultate
0 din 10 întrebări au răspunsuri corecte
Durată de răspuns:
Timpul a trecut
Ai obținut 0 din 0 de puncte posibile, (0)
| Scor mediu |
|
| Scorul tău |
|
Categorii
- Fără categorie 0%
-
-
Din păcate, nu ai răspuns corect de suficient de multe ori. Așa că nu ai primit nici un punct. Fii mai atent data viitoare.
| Poz. | Nume | Introdus pe | Puncte | Rezultat |
|---|---|---|---|---|
| Tabelul se încărcă | ||||
| Nicio dată disponibilă | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Cu răspuns
- Reia
-
Întrebarea 1 din 10
1. Întrebare
1 puncteCel mai mare număr par de forma cu cifre diferite esteCorect
Incorect
-
Întrebarea 2 din 10
2. Întrebare
1 puncteCorect
Incorect
-
Întrebarea 3 din 10
3. Întrebare
1 punctePătratul lui 4 esteCorect
Incorect
-
Întrebarea 4 din 10
4. Întrebare
1 puncteRezultatul calculului este egal cuCorect
Incorect
-
Întrebarea 5 din 10
5. Întrebare
1 puncteRezultatul calculului este egal cuCorect
Incorect
-
Întrebarea 6 din 10
6. Întrebare
1 puncteTriplul numărului este egal cuCorect
Incorect
-
Întrebarea 7 din 10
7. Întrebare
1 puncteDând factor comun în expresia , obținemCorect
Incorect
-
Întrebarea 8 din 10
8. Întrebare
1 puncte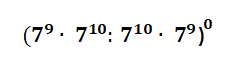 Corect
Corect
Incorect
-
Întrebarea 9 din 10
9. Întrebare
1 puncteRezultatul calculului 4+20:2 este egal cuCorect
Incorect
-
Întrebarea 10 din 10
10. Întrebare
1 puncteÎn calculul prima dată efectuămCorect
Incorect
Îți place quiz-ul făcut de acest user Kidibot?
Click să votezi!
Ne pare rău că un utilizator Kidibot a făcut un quiz atât de slab!
Probabil că a fost sabotat de către Crocobeți. Hai să-l îmbunătățim!
Spune-ne cum putem să-l îmbunătățim.
Exemple de întrebări din quizul "Lecția 2 – MULȚIMEA NUMERELOR NATURALE"
- Rezultatul calculului 4+20:2 este egal cu
- Rezultatul calculului este egal cu
- Rezultatul caaalculului este egal cu







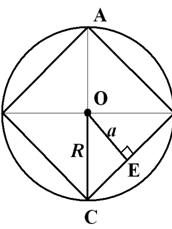 Cercul (4)
Cercul (4) INMULTIREA CU 81 !!!
INMULTIREA CU 81 !!! Numerele în chineză
Numerele în chineză Regatul de Gheata
Regatul de Gheata Proverbe internaționale
Proverbe internaționale Înmulțirea cu 2 – [5]
Înmulțirea cu 2 – [5] Sinonimele si antonimele
Sinonimele si antonimele Ștrumful și Jucăușul J – CLR cls I
Ștrumful și Jucăușul J – CLR cls I









